기술통계 (Descriptive Statistics)

4.통계분석

2절. 기초 통계 분석

1. 기술통계 (Descriptive Statistics)

가. 기술통계의 정의

자료를 요약하는 기초적 통계를 의미한다.
데이터 분석에 앞서 데이터의 대략적인 토계적 수치를 계산해 봄으로써 데이터에 대한 대략적인 이해와 앞으로 분석에 대한 통찰력을 얻기에 유리하다.
본격적인 데이터 분석에 앞서 데이터의 기술통계를 구해 보아야 한다.

# summary 함수 
# 데이터의 각 컬럼에 대해 볼 수 있다. 
# mean(평균), median(중앙값), sd(표준편차), var(분산), quantile(백분위수), min(최소값), max(최대값), 
# 데이터의 특정 컬럼을 선택할 떄는 "dataname%cloumn명" 

> summary(iris)
  Sepal.Length    Sepal.Width     Petal.Length    Petal.Width          Species  
 Min.   :4.300   Min.   :2.000   Min.   :1.000   Min.   :0.100   setosa    :50  
 1st Qu.:5.100   1st Qu.:2.800   1st Qu.:1.600   1st Qu.:0.300   versicolor:50  
 Median :5.800   Median :3.000   Median :4.350   Median :1.300   virginica :50  
 Mean   :5.843   Mean   :3.057   Mean   :3.758   Mean   :1.199                  
 3rd Qu.:6.400   3rd Qu.:3.300   3rd Qu.:5.100   3rd Qu.:1.800                  
 Max.   :7.900   Max.   :4.400   Max.   :6.900   Max.   :2.500                  
>

> sd(iris$Sepal.Length) # 표준편차 
[1] 0.8280661
> quantile(iris$Sepal.Length, 1/4) # 1사분위수 
25% 
5.1 
> quantile(iris$Sepal.Length, 3/4) # 3사분위수
75% 
6.4 

나. 통계량에 의한 자료 정리

1) 중심위치의 측도

자료 (data) : $X_1, X_2, ...., X_n$
표본평균(sample mean) : $\bar{X}= \frac{1}{n}(x_1+x_2+...+x_3) = \sum_{i=1}^{n}\frac{X_i}{n}$
중앙값(meadian) : 자료를 크기순으로 나열할 때 중앙에 위치하는 자료값

$\frac{(n+1)}{2}$ $n이 홀수 인 경우::: \frac{(n+1)}{2} \\ n이 짝수인 경우::: \frac{(n)}{2} 번째값 과 \frac{n}{2}+1 번째 값의 평균$

2) 산포의 측도

대표적인 산포도(dispersion)는 분산, 표준편차, 범위 및 사분위수 범위

분산 (variance)
- 편차는 음수와 0, 양수가 섞여 있다. 편차의 평균으로는 산포도를 알 수 없다.
- 편차 제곱의 평균, 편차를 전부 다 제곱해서 더한 다음 편차(변량)의 개수로 나눈다.
표준편차(standard deviation)
- 분산에 제곱근을 씌운 것, 양수인데 0이 될 수도 있다.
- 변량의 평균 -> 편차 -> 분산 -> 표준편차
사분위수범위(interquartle range)
- IQR=Q3-Q1
사분위수
- 제 1사분위수(Q1)= 25백분위수, 1/4
- 제 2사분위수(Q2)=50백분위수, 1/2
- 제 3사분위수(Q3)=75백분위수, 3/4
백분위수 (percentile) $\frac{(n-1)p}{100+1} 번쨰 값$
변동계수(coefficient of variation) $V=\frac{ S}{\bar{X}}$
평균의 표준오차

$SE(X)=\frac{S}{\sqrt{n}}$

3) 분포의 형태에 관한 측도

왜도(skewness) : skewness() - 분포의 비대칭 정도를 나타내는 측도이다.

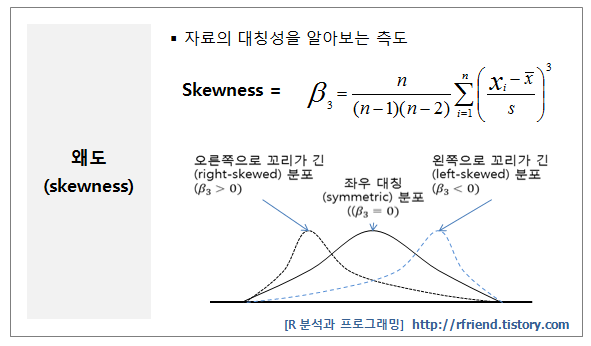
$m_3 = E\left [ (\frac{X-\mu}{\sigma})^3 \right ] = \frac{\mu_3}{\sigma^3}$

[이미지 참고 R분석과 프로그래밍]

(β3 > 0)

오른쪽으로 꼬리가 긴 분포 (right-skewed distribution)

왜도 점수가 ‘0’보다 크며
((β3 < 0)

왼쪽으로 꼬리가 긴 분포(left-skewed distribution)

왜도 점수가 ‘0’보다 작습니다.
기본적으로 관측값에서 평균을 뺀 값을 세제곱한 후에 더했기 때문입니다.

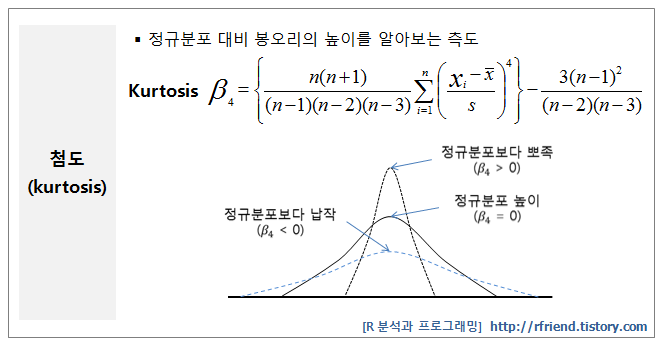
첨도 (kurtosis) : kurtosis()

분포의 중심에서 표쪽한 정도를 나타내는 측도 이다.
첨도(kurtosis)는 정규분포 대비 봉오리의 높이를 알아보는 측도입니다.
첨도가 ‘0’보다 크면 (β4 > 0) 정규분포보다 뾰족하다는 의미
첨도가 ‘0’보다 작으면 (β4 < 0) 정규분포보다 납작하다는 뜻
첨도(kurtosis, β4)는 데이터가 이봉분포(two mountaintop distribution)에 대해서 얼마나 단봉분포(one mountaintop distribution)에 가깝게 있는가를 판단하는데도 사용합니다

다. 그래프를 이용한 자료 정리

1. 히스토그램

표로 되어 있는 도수 분포를 그림으로 나타낸 것으로, 도수 분포표를 그래프로 나타낸 것이다.

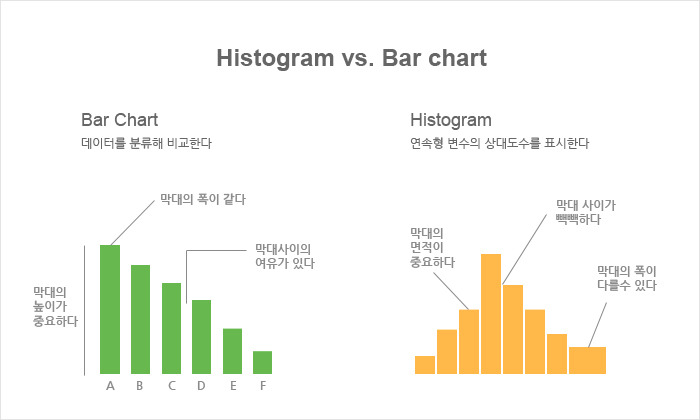
2. 막대그래프와 히스토그램의 비교

막대 그래프
- 범주형으로 구분된 데이터 (예, 직업, 종교, 음식) 을 표현하며 범주의 순서를 의도에 따라 바꿀 수 있다.
히스토그램
- 히스토 그램은 연속(continuous)형으로 표시된 데이터 (예: 몸무게, 성적, 연봉) 등을 표현하며
  
  임의로 순서를 바꿀 수 없고 막대의 간격이 없다.

3. 히스토그램의 생성 hist()

데이터 수를 활용해서 계급의 수와 계급 간격을 계산하여 도수분포표를 만들고 히스토그램을 생성한다.
계급의 수는 $2^k\ge n $ 을 만족하는 최소의 정수 $log_{2} n= k$ 에서 최소의 정수이다.

(k는 계급 수, n은 데이터 수)
계급의 간격은 (최대값- 최소값)/계급수 로 파악할 수 있다.
계급의 수와 간격이 변하면 히스토그램의 모양이 변한다.
R로 히스토그램 data 시각화 블로그 참조

hist(x, breaks=4, main="그래프제목")

4. 줄기-잎 그림(stem-and leaf plot) :데이터를 줄기와 잎의 모양으로 그린 그림

데이터의 수가 많지 않을 때 전체 데이터를 Stem과 Leaf으로 표현하는 플롯이다.

stem(x, scale = 1, width = 80, atom = 1e-08)

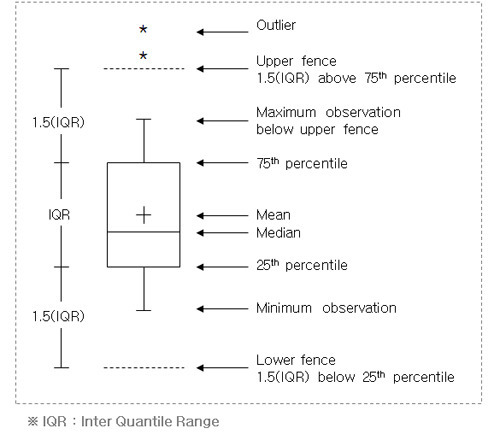
5. 상자그림 (Box plot)

중앙값, 제1사분위수, 제3사분위수 등의 기술통계량을 상자 모양으로 요약해서 나타낸 그래프이다.
상자의 크기는 제3사분위수-제1사분위수(q3-q1)으로 사분위수 범위(IQR)를 나타낸다.
사분위수 범위(iQR) :Q3~Q1
안울타리(inner fence) : Q ~ 1.5 x IQR 또는 Q3 +1.5 x IQR
바깥울타리(out fence) : Q1 ~3 x IQR 또느 Q3 x IQR
보통이상점 (mild outlier) : 안쪽 울타리와 바깥 울타리 사이에 있는 자료
극단이상점 (extreme outlier) : 바깥 울타리 밖의 자료
상자의 위 아래로 1.5*IQR을 넘어가는 부분은 이상치(outlier)로 표시

2. 인과관계의 이해

가. 용어

1) 종속변수(반응변수, y)

다른변수의 영향을 받는 변수

2) 독립변수(설명변수, x)

영향을 주는 변수

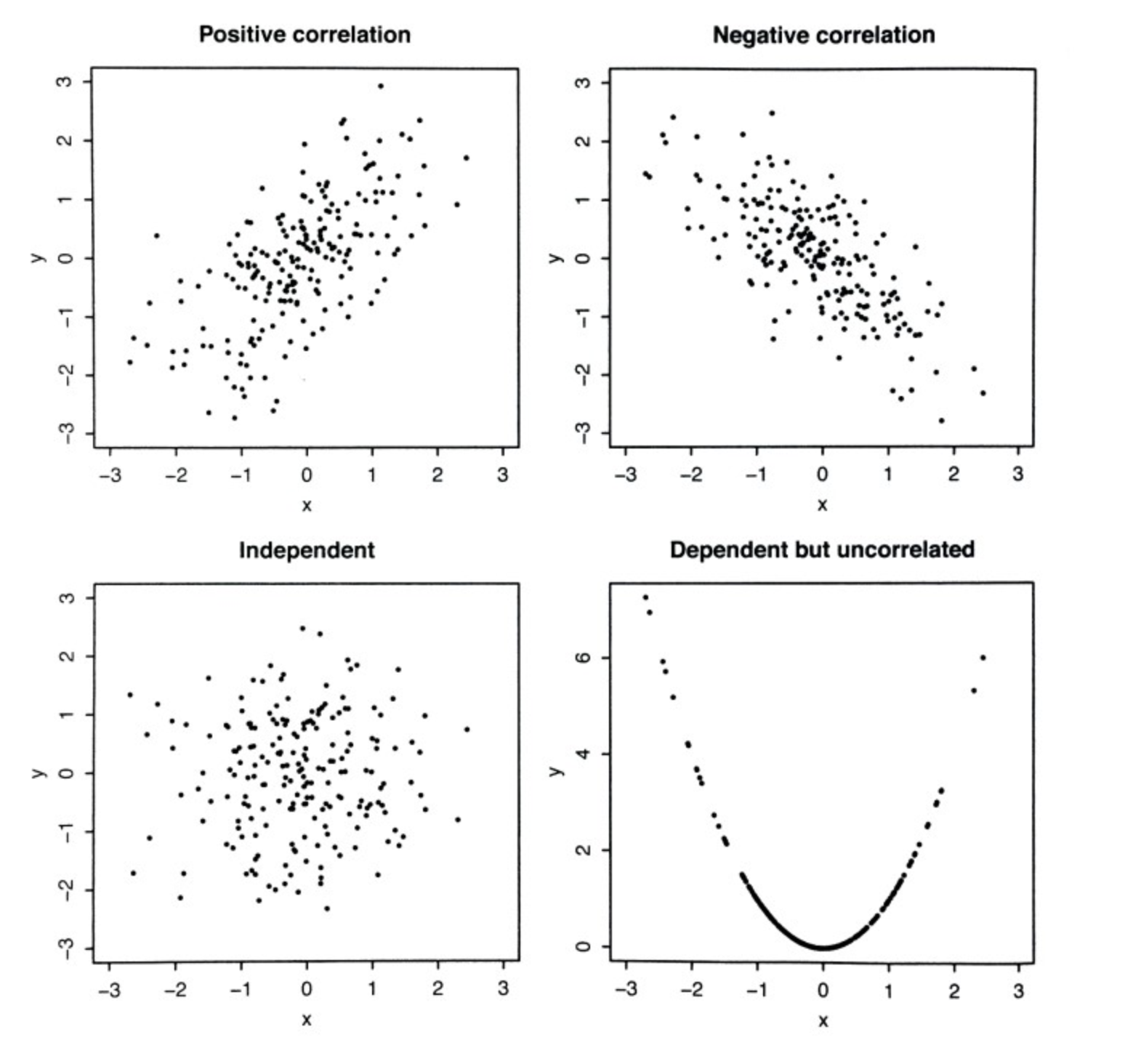
3) 산점도 (scatter plot)

x축과 y축으로 이루어진 그래프에 두 변수의 값을 점으로 나타낸 그래프이다.
산점도를 이용하면 두 변수의 관계를 파악하는데 용이하다.
산점도를 이용하면 값들이 얼마나 퍼져있는지(산포도)를 시각적으로 확인
이상값이 존재하는가?
몇개의 집단으로 구분(층별) 되는가?
두 변수 사이의 선형관계(직선)가 성립하는가?

나. 공분산(covariance)

두 확률변수 $X$, $Y$ 의 방향의 조합이 선형성이다.
$Cov(X,Y) = E[(X-\mu_{x})(Y-\mu_{r})]$
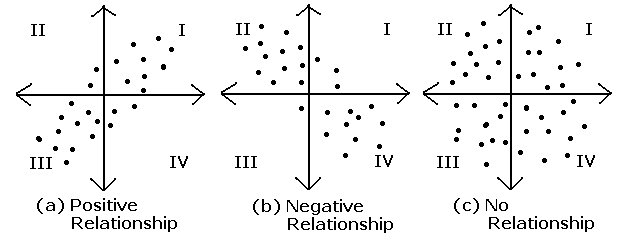
공분산의 부호만으로 두 변수간의 방향성을 확인할 수 있다.
공분산의 부호가 $ + $이면 두 변수는 양의 방향성, 공분산의 부호가$ - $ 이면 음의 방향성을 가진다.
$Cov(X, Y) > 0 $ $X$가 증가 할 때$ Y$도 증가한다.
$Cov(X, Y) < 0$ $X$가 증가 할 때$ Y$는 감소한다.
$X$,$Y$ 가 서로 독립이면, $Cov(X,Y)=0$ 이다.
아무런 선형관계가 없으며 두 변수는 서로 독립적인 관계에 있음을 알 수 있다.

3. 상관 분석 (Correalation Analysis)

가. 상관분석의 정의

두 변수 간의 관계의 정도를 알아보기 위한 분석방법이다.
두 변수의 상관관계를 알아보기 위해 상관계수를 이용하며, 그 공식은 아래와 같다.
상관 계수 값의 범위는 -1 부터 +1까지이다. 계수의 절대값이 클 수록 변수 사이에 강한 관계가 있다.
pearson 상관의 경우 절대값은 1 완전한 선형관계를 나타낸다.
0에 가까운 상관 값은 변수 사이에 선형관계가 없음을 나타낸다.

$r=\frac{cov(x,y)}{S_{x}\times S_{y}} =\frac{\sum_{i=1}^{n} \left [(x-\bar{x})(y-\bar{y}) \right ]}{n(S_{x}\times S_{y})}$

나. 변수 사이의 관계의 강도 및 방향

- 아무런 관계도 없음: Pearson r = 0

점들이 그림에 랜덤하게 위치합니다. 이는 변수 사이에 선형 관계가 없다는 것을 나타냅니다.

- 적절한 양의 관계: Pearson r = 0.476

일부 점은 선에 가깝고 일부 점은 선에서 멀리 떨어져 있습니다. 이는 변수 사이에 적절한 선형 관계만 있다는 것을 나타냅니다.

- 강한 양의 관계: Pearson r = 0.93

점들이 선에 가깝게 위치합니다. 이는 변수 사이에 강한 선형 관계가 있다는 것을 나타냅니다. 한 변수가 증가하면 다른 변수도 증가하기 때문에 양의 관계가 있습니다.

- 강한 음의 관계: Pearson r = −0.968

점들이 선에 가깝게 위치합니다. 이는 변수 사이에 강한 음의 선형 관계가 있다는 것을 나타냅니다. 한 변수가 증가하면 다른 변수도 감소하기 때문에 음의 관계가 있습니다.

상관 계수만을 기초로 하여 한 변수의 변화가 다른 변수의 변화를 유발한다는 결론을 내리는 것은 적절하지 않습니다. 적절히 통제된 실험에서만 인과 관계를 확인할 수 있습니다.
Pearson 상관 계수는 극단 데이터 값의 영향을 상당히 많이 받습니다. 데이터 집합에 나머지 값들과 매우 다른 값이 하나 있으면 상관 계수의 값이 크게 변경될 수 있습니다. 따라서 극단값의 원인을 식별해야 합니다. 모든 데이터 입력 또는 측정 오류를 수정합니다. 비정상적인 일회성 사건과 연관된 데이터 값을 삭제합니다(특수 원인). 그런 다음 분석을 반복합니다.
낮은 Pearson 상관 계수는 변수 사이에 관계가 없다는 것을 의미하지 않습니다. 변수 사이에 비선형 관계가 있을 수도 있습니다. 비선형 관계를 그래픽으로 확인하려면 산점도을 생성하거나 적합선 그림을 사용하십시오.

다. 상관분석의 유형

구분	피어슨(Pearson)	스피어만(Spearman)
개념	- 등간척도 이상으로 측정된 두 변수들의 상관 관계 특정 방식	- 서열척도인 두 변수들의 상관관계 측정방식
특징	- 연속형 변수, 정규성 가정 - 대부분 많이 사용	- 순서형 변수, 비모수적 방법 - 순위를 기준으로 상관관계 측정
상관계수	- 피어슨 $\gamma$ (적률상관계수)	- 순위상관계수($\rho$ ,로우)

라. 상관분석을 위한 R코드

구분	R code
분산	var(x,y=Null, na.rm=FALSE)
공분산	cov(x,y=NULL, use=”everything”, method=c(“pearson”, “kendall”, “spearman”))
상관관계	cor(x,y=NULL, use=”everything”, method=c(“pearson”, “kendall”, “spearman”))

마. 상관분석의 가설 검정

상관계수 $\gamma$ 이 0이면 입력변수 x와 출력변수 y사이에는 아무런 관계가 없다.

(귀무가설 : $\gamma = 0$ , 대립가설 $\gamma \neq 0$)
t 검정 통계량을 통해 얻은 p-valu값이 유의수준 ($\alpha$ ,0.05의 유의수준) 이하인 경우, 대립가설을 채택하게 되어 우리가 데이터를 통해 구한 상관계수를 활용할 수 있게 된다.
p-값 ≤ α: 상관 관계가 통계적으로 유의합니다.

p-값이 유의 수준보다 작거나 같으면 상관 계수가 0과 다르다는 결론을 내릴 수 있습니다.
p-값 > α: 상관 관계가 통계적으로 유의하지 않습니다.

p-값이 유의 수준보다 크면 상관 관계가 0과 다르다는 결론을 내릴 수 없습니다.

바. 상관분석 예제

> # "mtcars"라는 데이터셋 
> # 마일(mpg), 총마력(hp) 의 상관관계 분석을 실시한다. 

> data(mtcars)
# 마일 (mpg) 데이터 셋 a로 정의 
> a <-mtcars$mpg
# 총마력(hp) b 로 정의 
> b <-mtcars$hp

> # 공분산 
> cor(a,b)
[1] -0.7761684
> # 상관계수
> cov(a,b)
[1] -320.7321

> # a, b(마일과 총마력) 상관관계 분석 
> cor.test(a, b, method="pearson")

	Pearson's product-moment
	correlation

data:  a and b
t = -6.7424, df = 30, p-value =
1.788e-07
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 -0.8852686 -0.5860994
sample estimates:
       cor 
-0.7761684  

> 

공분산은 -0.7761684 , 상관계수는 -320.7321 따라서 mpg와 hp는 공분산으로 음의 방향성을 가지는 것은 알 수 있다.
상관계수를 보면 강한 음의 상관관계가 있음을 알 수 있다.
cor.test를 이용해 mpg와 hp의 상관관계 분석을 실행한 결과
p-value 1.788e-07 로 유의 수준 0.05보다 작게 나타나므로 mpg와 hp가 상관관계가 있다고 할 수 있다.