기초통계분석 (Data Statistical Analysis)

4장 통계분석

1절 통계분석의 이해

1. 통계

• 특정집단을 대상으로 수행한 조사나 실험을 통해 나온 결과에 대한 요약된 형태의 표현
• 조사 또는 실험을 통해 데이터를 확보, 조사대상에 따라 총조사(census)와 표본조사로 구분한다.

2. 통계자료의 획득 방법

가. 총 조사/전수조사 (census)

• 대상 집단 모두를 조사하는데 많은 비용과 시간이 소요되므로 특별한 경우를 제외하고는 사용되지 않는다. (인구주택 총 조사)

나. 표본조사

• 대부분의 설문조사가 표본조사로 진행되며 모집단에서 샘플을 추출하여 진행하는 조사이다.

• 모집단(population): 조사하고자 하는 대상 집단 전체

• 원소(element): 모집단을 구성하는 개체

• 표본(sample): 조사하기 위해 추출한 모집단의 일부 원소

• 모수(parameter): 표본 관측에 의해 구하고자 하는 모집단에 대한 정보 , 모집단의 통계값 _ex.모평균 μ, 모표준편차 σ, 모비율 p

• 모집단의 정의, 표본크기, 조사방법, 조사기간, 표본 추출방법을 정확히 명시해야 한다.

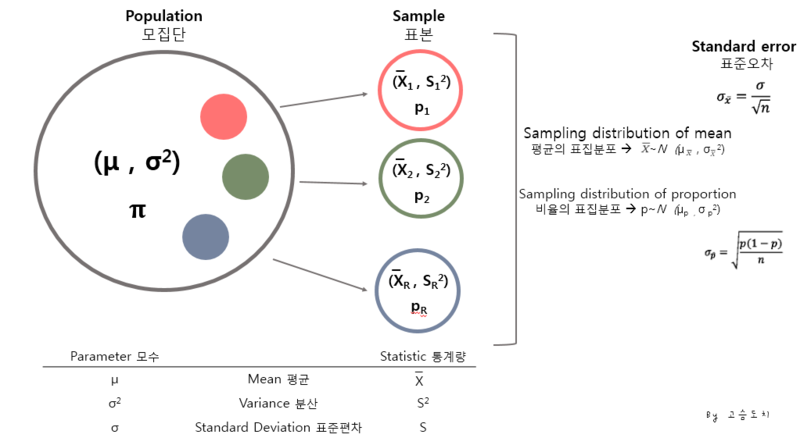
• Statistic(통계량) : 표본의 통계값_ ex.표본의 평균 x̄, 표본 표준편차
• Standard deviation(표준편차) : 분산의 제곱근, 통계집단의 변수가 평균을 중심으로 얼마나 퍼져 있는지를 나타내는 대표적인 분포도 지수
• Sampling distribution of mean(평균의 표집분포) : 같은 모집단에서 n크기의 표본을 무한 반복하여 뽑아서 추정한 표본 평균값의 분포
• Standard error(표준오차) : 표본평균이 모평균과 얼마나 퍼져 있는지를 나타내는 표준편차 추정치

다. 표본 추출 방법

*** 표본추출법 4가지 방법과  용어를 정확히 알도록 한다.

• 표본 조사의 중요한 점은 모집단을 대표할 수 있는 표본 추출이므로 표본 추출 방법에 따라 분석결과의 해석은 큰 차이가 발생한다.
  1. 단순랜덤 추출범(simple random sampling)
     • 각 샘플에 번호를 부여하여 임의의 n개를 추출하는 방법으로 각 샘플은 선택될 확률이 동일하다. (비복원, 복원(추출한 element를 다시 집어 추출하는 경우) 추출)
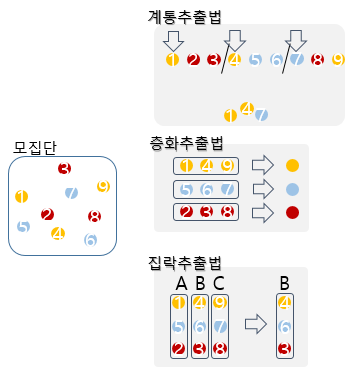
  2. 계통 추출법(systematic sampling)
     • 단순랜덤추출법의 변형된 방식으로 번호를 부여한 생픔을 나열하여 k개씩(K=N/n) n개의 구간으로 나누고 첫 구간(1,2,…,K) 에서 하나를 임의로 선택한 후에 k개씩 띄어서 n개의 표본을 선택한다. 즉, 임의 위치에서 매 k번째 항목을 추출하는 방법이다.
  3. 집락추출법(cluster random sampling)
     • 군집을 분류하고 군집별로 단순랜덤 추출법을 수행한 수, 모든 자료를 활용하거나 샘플링 하는 방법이다. (지역표본추출, 다단계표본추출)
  4. 층화추출법(startified sampling)
     • 이질적인 원소들로 구성된 모집단에서 각 계층을 고루 대표할 수 있도록 표본을 추출하는 방법으로, 유사한 원소끼리 몇 개의 층(stramtum)으로 나누어 각 층에서 랜덤 추출하는 방법이다.
     • (비례층화추출법, 불비례층화추출법)

라. 측정(measurement)

1. 개요

   • 표본조사나 실험을 실시하는 과정에서 추출된 원소들이나 실험 단위로부터 주어진 목적에 적합하도록 관측해 자료를 얻는 것이다.

2. 측정방법

측정 방법	내용
명목척도 (nominal scale)	측정 대상이 어느 집단에 속하는지 분류할 때 사용 (성별, 출생지 구분)	질적척도 (범주형자료, 숫자들의 크기차이가 계산되지 않는 척도)
순서척도 (ordinal scale)	측정 대상의 서열관계를 관측하는 척도 (만족도, 선호도, 학년, 신용등급)	질적척도 (qualitative data)
구간척도 (interval scale)	측정 대상이 갖고 있는 속성의 양을 측정하는 것으로 구간이나 구간 사이의 간격이 의미가 있는 자료 (온도, 지수)	양적척도 (수치형자료, 숫자들의 크기 차이를 계산 할 수 있는 척도)
비율척도 (ratio scale)	간격(차이)에 대한 비율이 의미를 가지는 자료, 절대적 기준인 0이 존재하고 사칙연산이 가능하며 제일 많은 정보를 가지는 척도 (무게, 나이,연간소득, 제품가격 시간, 거리)	양적척도 quantitative data

• 서열척도는 명목척도와 달리 매겨진 숫자의 크기를 의미있게 활용할 수 있다.

  (예: 1등이 2등보다는 성적이 높다.)

• 구간척도는 절대적 크기는 측정할 수 없기 때문에 사칙연산 중 더하기와 빼기는 가능하지만 비율처럼 곱하거나 나누는 것은 불가능하다.

3. 통계분석 (Statistical Analysis)

가. 정의

• 특정한 집단이나 불확실한 현상을 대상으로 자료를 수집해 대상 집단에 대한 정보를 구하고, 적절한 통계분석 방법을 이용해 의사결정을 하는 과정이다.

나. 기술통계(descriptive statistics)

• 주어진 자료부터 어떠한 판단이나 예측과 같은 주관이 섞일 수 있는 과정을 배제하여 통계집단들의 여러특성을 수량화하여 객관적인 데이터로 나타내는 통계분석 방법론이다.
• Sample에 대한 특성인 평균, 표준편차, 중위수, 최빈값, 그래프, 왜도, 첨도 등을 구하는 것을 의미한다.

다. 통계적 추론(추측통계, inference statistics)

• 수집된 자료를 이용해 대상 집단(모집단)에 대한 의사결정을 하는 것으로 sample을 통해 모집단을 추정하는 것을 의미한다.

1. 모수추정
   • 표본집단으로부터 모집단의 특성인 모수 (평균, 분산등) 를 분석하여 모집단을 추론한다.
2. 가설검정
   • 대상집단에 대해 특정한 가설을 설정한 후에 그 가설이 옳은지 그른지에 대한 채택여부를 결정하는 방법론이다.
3. 예측
   • 미래의 불확실성을 해결해 효율적인 의사결정을 의사결정을 하기 위해 활용한다.
   • 회귀분석, 시계열분석 등이 방법이 있다.

4. 확률 및 확률분포

가. 확률

• '’특정사건이 일어날 가능성의 척도’’ 라고 정의할 수 있다.

• 모든 결과들의 집합을 표본공간 (Sample Space, $\Omega $)이라고 하고 , 사건(event)란 표본공간의 부분집합을 말한다.

• 표본공간 $S$ 에 부분집합인 각 사상에 대해 실수값을 가지는 함수의 확률값이 0과 1사이에 있고, 전체 확률의 합이 1인 것을 의미한다. 표본공간 $\Omega$ 의 부분집합인 사건 $E$ 의 확률은 표본공간의 원소의 개수에 대한 사건 $E$ 의 개수의 비율로 확률을 $P(E)$ 라고 할 때, 다음과 같이 정의한다.

$$P(E) = \frac{n(E)}{n(\Omega)}$$

• 일반적으로 확률은 표본공간의 부분집합에 실수값을 지정한 것으로 다음과 같은 세 가지 조건을 만족한다.

  1. 모든 사건 $E$ 의 확률값은 0과 1사이에 있다. 즉, $ 0 \le P(E) \le 1$

  2. 전체 집합 $\Omega$ 의 확률은 1이다. 즉, $P(\Omega)=1$

  3. 서로 배반인 사건들 $E_{1}, E_{2}…$ 의 합집합의 확률은 각 사건들의 확률의 합이다. 즉, 배반 사건이란, 교집합이 공집합인 사건들을 말한다.

  $$P( \cup E_{ n })=\sum _{ n=1 }^{ \infty }{ P(E_{ n } }$$

나. 조건부 확률과 독립사건

• 사건 A가 일어 났다는 가정하의 사건 B의 확률을 조건부 확률 (conditional provavility)라 한다.

• 사건 A가 주어졌을 때 조건부 확률은 $P(B

  A)$와 같이 표시하고, 다음과 같이 정의된다.

$$P(B|A)=\frac { P(A\cap B) }{ P(A) }$$

• 위의 확률은 $P(A)>0$ 일 때만 정의가 된다.
• 독립사건, 두 사건 $A, B$ 가

$$P(A \cap B) = P(A)P(B)$$

• 를 만족하면, 서로 독립이라고 한다.
• 두 사건 $A, B$가 독립이면, $P(B|A)=P(B)$ 가 된다. 따라서 사건 $B$의 확률은 $A$가 일어났다는 가정하에서 $B$의 조건부 확률과 동일하다. 즉, 사건 $B$의 확률은 사건 $A$가 일어났는지 여부와 상관없이 동일하다.

다. 확률분포

• 통계분석에서 자료를 수집하고 그 수집된 자료로부터 어떤 정보를 얻고자 하는 경우에는 항상 수집된 자료가 특정한 확률분포를 따른다고 가정한다. 그 분포는 이산형 확률분포와 연속형 확률 변수로 구분할 수 있다.

• 확률변수(random variable)
  • 특정 사건에 대해 실수값을 갖는 변수를 정의한다.
  • 특정사건이 일어날 확률은 그 변수가 특정값을 가질 확률로 표현할 수 있다.
  • 이와 같이 특정값이 나타날 가능성이 확률적으로 주어지는 변수를 말한다.
  • 정의역(domain)이 표본공간이고 치역(range)이 실수값(0<y<1)인 함수이다.
• 이산형 확률변수 (discrete random variable)
  • 사건의 확률이 그 사건들이 속한 점들의 확률의 합으로 표현할 수 있는 확률변수를 말한다.
  • 이산형 확률변수는 확률이 0보다 큰 값을 갖는 점들로 확률을 표현할 수 있다.

$$P(X =x_{i})=p_{i} , i=1 ,2, ...$$

• 베르누이 확률분포(Bernoulli distribution), 이항분포(biomial distribution), 기하분포(geometri distribution), 다항분포(multinomial distribution), 포아송분포(Poisson distribution)

• 연속형 확률변수 (continuous random varivble)

  • 사건의 확률이 그 사건 위에서 어떤 $0$보다 큰 값을 갖는 함수의 면적으로 표현 될 수 있는 확률변수를 말한다.

  • 이 때, 함수 $ f(x)$ 를 확률밀도함수(provavility density function) 라고 한다.

  • 사건의 확률이 확률밀도함수의 면적으로 표현되므로 한 점에서의 확률은 0이 되고, $0$보다 큰 값을 갖는 사건은 구간에서 확률값이 된다.

$$P(X=x_i, Y=y)=p_{ij} , i=1, 2, ..., n, j=1, 2, ..., m$$

• 균일분포(uniform distribution, 정규분포(normal distribution), 지수분포(exponential) , 정규분포로부터 유도된 t-분포(t-distribution) , $X^{2}$ - 분포($X^{2}$ - distribution), F-분포 (F-distribution) 등이 있다.

라. 확률변수의 기댓값과 분산

• 확률변수 $X$의 기대값은 다음과 같이 정의 된다. 확률변수 $X$가 확률질량함수 $f(x)$를 갖는 이산형 확률변수인 경우,
• 그 기댓값은

$$E(X) = \sum xf(x)$$

• 같이 정의되고, $X$ 가 확률밀도함수 $f(x)$를 갖는 연속형 확률변수인 경우에는

$$E(X)= \int xf(x)dx$$

• 와 같이 정의 된다. 확률변수의 흩어진 정도를 나타내는 분산과 표준편차는 $X$의 기댓값을 $\mu$ 라 할 때, 다음과 같이 정의 한다.

$$\begin{matrix} { Var(X)=E(X-\mu )^{ 2 } }\\{ sd(X)= \sqrt { Var(X)} } \end{matrix}$$

마. 백분위수

• 연속형 확률변수 $X$의 제 $q$ 백분위수 $x_q$ 는 다음의 식을 만족하는 값으로 정의 된다.

$$P(X\leq x_q)=q/100$$

• 여기서 $q$는 0과 100사이의 값이다.

4. 추정과 가설검정

• 통계적 방법론을 통해 알고자 하는 대상은 모집단의 확률분포이다.
• 모집단의 확률분포의 특징을 표현하는 값들을 모수(parameter)라고 한다. 대표적인 모수의 예는 모집단의 평균, 분산, 표준편차, 백분위수 등이 있다.
• 모집단에서 추출된 표본을 기반으로 모수들에 대한 통계적 추론을 한다.
• 통계적 추론은 추정과 가설검정으로 나뉘고,
• 추정은 다시 점추정과 구간 추정으로 나뉜다.

가. 점추정 (point estimation)

• 가장 참값이라고 여겨지는 하나의 모수의 값을 택하는 것을 점추정 (point estimation)이라고 한다.

• ‘모수가 특정한 값일 것’이라고 추정하는 것이다.

• 표본의 평균, 중위수 , 최빈값 등을 사용한다.

• 표본 평균 - 모집단의 평균(모평균) $\mu$ 를 추정하기 위한 추정량(estimator)은 확률표본의 평균값인 표본평균(sample mean)이 대표적이다.

$$\bar { X }=\frac{1}{n}\sum _{i=1}^{ n }{(X_i-\bar{X})^2 }$$

• 표본분산 - 모집단의 분산(모분산) $σ^2$ 를 추정하기 위한 추정량으로는 표본분산(sample variance)이 대표적이다.

$$S^2 = \frac{1}{n-1}\sum_{i=1}^{n}{(X_i-\bar{X})^2}$$

나 . 구간추정

• 점추정이 정확성을 보완하기 위해 확률로 표현된 믿음을 정도 하에서 모수가 특정한 구간에 있을것이라고 선언하는 것이다.

• 일정한 크기의 신뢰수준(confidence level)으로 모수가 특정한 구간에 있을 것이라고 선언하는 것으로, 구해진 구간을 신뢰구간(comgidence interval)이라고 한다.

• 일반적으로 신뢰수준은 90%, 95%, 99%의 확률을 이용하는 경우가 많다.

  • 95% 신뢰 수준하에서 모평균의 신뢰 구간

  • 모분산 $\sigma^2$ 이 알려져 있는 경우

$$\left ( \bar{X}-1.96 \frac{\sigma}{\sqrt{n}}, \bar{X}+1.96 \frac{\sigma}{\sqrt{n}} \right )$$

• 모분산이 $\sigma^2$이 알려져 있지 않은 경우에는 모분산 대신 표본분산을 사용

$$\left ( \bar{X}-t_{n-1,0.975}\frac{S}{\sqrt{n}}, \bar{X}+t_{n-1,0.975} \frac{S}{\sqrt{n}} \right )$$

• 여기서 $t_{n-1,0.975}$ 는 자유도가 $n-1$ 인 t-분포를 따르는 t분포의 97.5 백분위수이다.

$$T= \frac{\bar{X}-\mu}{S/\sqrt{n}}$$

다. 가설검정

• 모집단에 대한 어떤 가설을 설정한 뒤에 표본관찰을 통해 그 가설의 채택 여부를 결정하는 분석방법
• 표본 관찰 또는 실험을 통해 귀무가설과 대립가설 중에서 하나를 선택하는 과정이다.
• 검정하고자 하는 모집단의 모수에 대한 가설 설정이다.
• 귀무가설이 옳다는 전제하에 검정 통계량 값을 구한 후에 이 값이 나타날 가능성이 크기에 의해 귀무가설 채택여부를 결정한다.

1. 귀무가설 (null hypothesis, $H_0$)

   • 대립가설과 반대의 증거를 찾기 위해 정한 가설
   • ‘‘비교하는 값과 차이가 없다. 동일하다’‘ 를 기본개념으로 하는 가설

2. 대립가설 (alternative hypothesis, $H_1$)

   • 확실하게 증명하고 싶은 가설, 뚜렷한 증거가 있어야 채택할 수 있는 가설
   • 혹은 그 결과가 값비싼 가설을 대립가설이라한다.

3. 검정통계량(test statistic, $T(X)$)

   • 관찰된 표본으로부터 구하는 통계량, 검정 시 가설의 진위를 판단하는 기준

4. 유의수준(significance level, $\alpha $)

   • 미리 주어진 기준값인 유의수준 보다 작으면 귀무가설이 나올 가능성이 적다고 판단해 귀무가설을 기각한다.
   • 보통 0.01, 0.005, 0.1중 한 개의 값을 사용한다.

5. 기각역(ciritical retgion, $C$)

   • 귀무가설을 기각하는 통계량의 영역
   • 귀무가설이 옳다는 전제하에 구한 검정통계량의 분포에서 확률이 유의수준인 $\alpha$인 부분

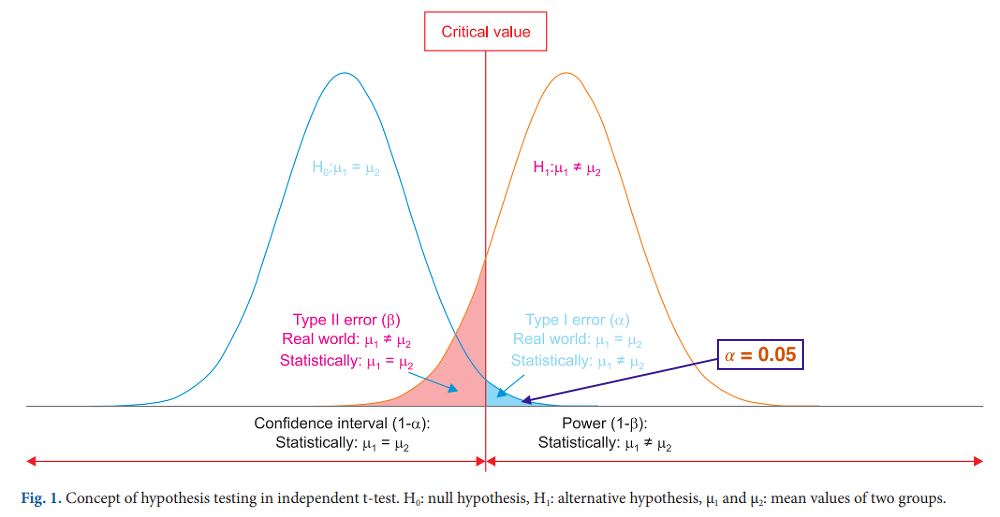
<95% 신뢰구간에서 실험 $(1-\alpha)=0.95$>

귀무가설 $(H_0): \mu_{1}=\mu_{2}$	T통계량	P-value
대립가설 $(H_0): \mu_{1}\neq\mu_{2}$	(10.248)	(0.0001)

<1종오류와 2종오류 >

	$H_0$가 사실이라고 판정	$H_0$가 사실이 아니라고 판정
$H_0$가 사실임	옳은 결정	제 1종오류 $(\alpha)$
$H_0$가 사실이 아님	제 2종오류 $(\beta)$	옳은 결정

• 1종 오류(type I error) - 귀무가설$H0$이 옳은데도 귀무가설$H0$ 을기각하게 되는 오류

• 2종 오류(type II error) - 귀무가설$H0$ 가 옳지 않은데도 귀무가설$H0$ 을 채택하게 되는 오류

• 두 가지 오류는 서로 상충관계가 있어서 일반적으로 가설검정에서는 제 1종 오류 $\alpha$ 의 크기를 0.1, 00.5, 0.01등으로 고정시킨 뒤 제 2종 오류 $\beta$ 가 최소가 되도록 기각역을 설정한다.

라. 비모수 검정

• 통계적 검정에서 모집단의 모수에 대한 검정에는 모수적 방법(parametric method)과 비모수적 방법(nonoparameteric method)이 있다.

• 모수적 검정 방법
  • 검정하고자 하는 모집단의 분포에 대한 가정을 하고, 그 가정하에서 검정통계량과 검정 통계량의 분포를 유도해 검정을 실시하는 방법이다.
• 비모수적 검정 방법
  • 자료가 추출된 모집단의 분포에 대해 아무 제약을 가하지 않고 검정을 실시하는 검정방법

  • 관측된 자료가 특정 분포를 따른다고 가정할 수 없는 경우에 이용된다.

  • 관측된 자료의 수가 많지 않거나 (30개미만) 자로가 개체간의 서열관계를 나타내는 경유에 이용한다.

<비모수 검정과="" 모수="" 검정의="" 차이점="">

• 가설의 설정
  • 모수적 검정에서는 가정된 분포의 모수 (모평균$\mu$, 모비율 $p$ 모분산 $\sigma^{2}$ 등)에 대해 가설을 설정한다.
  • 비모수 검정에서는 가정된 분포가 없으므로 가설은 단지 ‘분포의 형태가 동일하다’, 또는 ‘분포의 형태가 동일하지 않다.’ 와 같은 분포의 평태에 대해 설정한다.
• 검정 방법
  • 모수적 검정에서는 관측된 자료를 이용해 구한 표본평균$\bar{X}$ , 표본분산$S^{2}$ 등을 이용해 검정을 실시한다.
  • 비모수 검정에서는 관측값의 절대적인 크기에 의존하지 않는 관측값들의 순위(rank)나 두 관측값 차이의 부호 등을 이용해 검정한다.
• 비모수 검정의 예
  • 부호검정(sign test), 월콕슨의 순위합검정(rank sum test), 윌콕슨의 부호순위합검정(signed rank test), 만-위트니의 U검정, 런검정(run test), 스피어만의 순위상관계수